Bukti Menentukan Jari-Jari Lingkaran Dalam Segitiga

Berhubungan dengan post Lingkaran Luar Segitiga. Sekarang kita akan menentukan bagaimana cara menentukan panjang jari-jari lingkaran dalam (inradius) dari suatu segitiga...

Diberikan sebuah segitiga dengan sisi a, b, dan c.

Dengan demikian, jari-jari lingkaran dalam segitiga tersebut dapat ditentukan sbb:

dimana

Bukti dari rumus ini justru sangat mudah.. Lihat lanjutannya..
=========================================================================

BUKTI

Kembali gambarkan segitiga ABC seperti berikut:

Kita tahu bahwa luas total segitiga dapat dicari dengan penjumlahan dari luas segitiga ABO, BCO, dan ACO.. Maka, dengan menjumlahkannya dan memisahkan bagian R (jari-jari), maka rumus tersebut akan terbukti. Untuk lebih jelasnya, akan dijabarkan di sini.

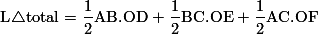
Kita tahu bahwa , maka:

Kita dapatkan rumus untuk mencari inradius sbb:

Kita masih bisa membentuk rumus di atas dengan bentuk yang lain.
Sesuai dengan formula Heron yang dibahas di post INI yang menyatakan bahwa: Luas segitiga = \sqrt{s(s-a)(s-b)(s-c)}, di mana s=\frac{1}{2}{a+b+c}, maka rumus tersebut dapat dibentuk sbb:

TERBUKTI

=========================================================================
Sekian post yang terbilang singkat ini.. Lihat juga poat yang akan datang selanjutnya... ^^